-
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
-
К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
-
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом \(r = 1\). На окружности обозначена точка \(M\left( {x,y} \right)\). Угол между радиус-вектором \(OM\) и положительным направлением оси \(Ox\) равен \(\alpha\).

-
Синусом угла \(\alpha\) называется отношение ординаты \(y\) точки \(M\left( {x,y} \right)\) к радиусу \(r\): \(\sin \alpha = y/r\). Поскольку \(r = 1\), то синус равен ординате точки \(M\left( {x,y} \right)\).
-
Косинусом угла \(\alpha\) называется отношение абсциссы \(x\) точки \(M\left( {x,y} \right)\) к радиусу \(r\): \(\cos \alpha = x/r\)
-
Тангенсом угла \(\alpha\) называется отношение ординаты \(y\) точки \(M\left( {x,y} \right)\) к ee абсциссе \(x\): \(\tan \alpha = y/x,\;\;x \ne 0\)
-
Котангенсом угла \(\alpha\) называется отношение абсциссы \(x\) точки \(M\left( {x,y} \right)\) к ее ординате \(y\): \(\cot \alpha = x/y,\;\;y \ne 0\)
-
Секанс угла \(\alpha\) − это отношение радиуса \(r\) к абсциссе \(x\) точки \(M\left( {x,y} \right)\): \(\sec \alpha = r/x = 1/x,\;\;x \ne 0\)
-
Косеканс угла \(\alpha\) − это отношение радиуса \(r\) к ординате \(y\) точки \(M\left( {x,y} \right)\): \(\csc \alpha = r/y = 1/y,\;\;y \ne 0\)
-
В единичном круге проекции \(x\), \(y\) точки \(M\left( {x,y} \right)\) и радиус \(r\) образуют прямоугольный треугольник, в котором \(x,y\) являются катетами, а \(r\) − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: Синусом угла \(\alpha\) называется отношение противолежащего катета к гипотенузе. Косинусом угла \(\alpha\) называется отношение прилежащего катета к гипотенузе. Тангенсом угла \(\alpha\) называется противолежащего катета к прилежащему. Котангенсом угла \(\alpha\) называется прилежащего катета к противолежащему. Секанс угла \(\alpha\) представляет собой отношение гипотенузы к прилежащему катету. Косеканс угла \(\alpha\) представляет собой отношение гипотенузы к противолежащему катету.
-
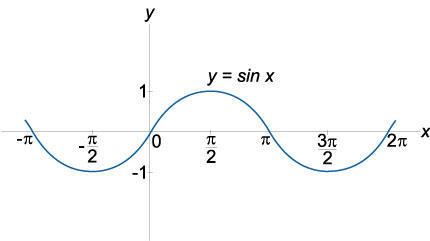
График функции синус \(y = \sin x\), область определения: \(x \in \mathbb{R}\), область значений: \(-1 \le \sin x \le 1\)
-
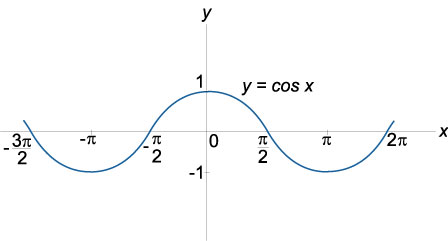
График функции косинус \(y = \cos x\), область определения: \(x \in \mathbb{R}\), область значений: \(-1 \le \cos x \le 1\)
-
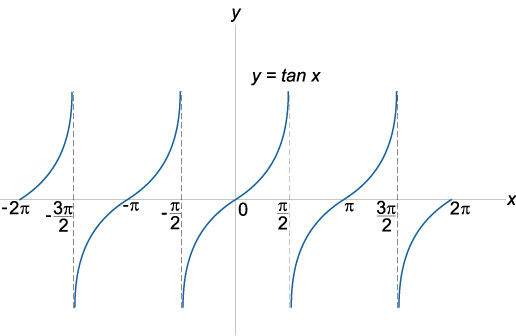
График функции тангенс \(y = \tan x\), область определения: \(x \in \mathbb{R}, x \ne \left( {2k + 1} \right)\pi/2\), область значений: \(- \infty <\tan x<\infty\)
-
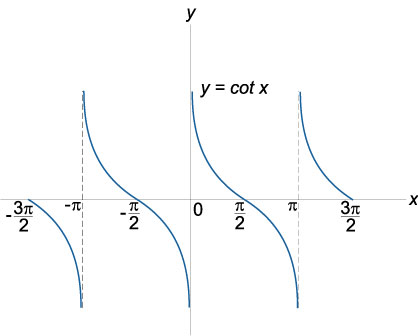
График функции котангенс \(y = \cot x\), область определения: \(x \in \mathbb{R}, x \ne k\pi\), область значений: \(- \infty <\cot x<\infty\)
-
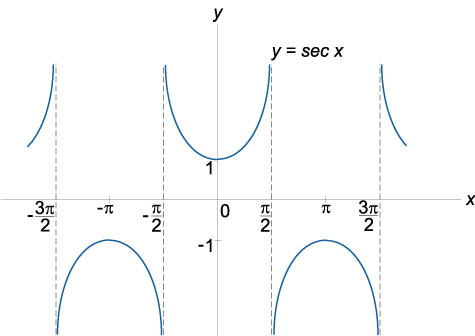
График функции секанс \(y = \sec x\), область определения: \(x \in \mathbb{R}, x \ne \left( {2k + 1} \right)\pi/2\), область значений: \(\sec x \in \left( {-\infty , -1} \right] \cup \left[ {1,\infty } \right)\)
-
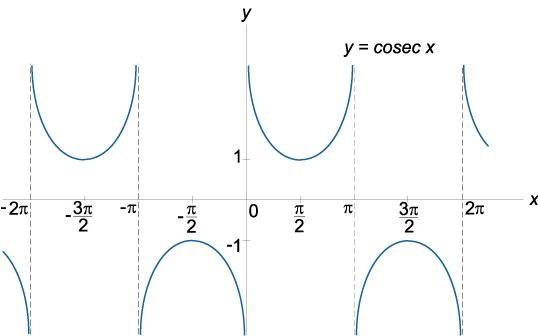
График функции косеканс \(y = \csc x\), область определения: \(x \in \mathbb{R}, x \ne k\pi\), область значений: \(\csc x \in \left( {-\infty , -1} \right] \cup \left[ {1,\infty } \right)\)