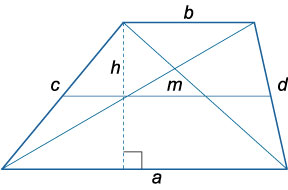
Трапецией называется четырехугольник, у которого две противоположные стороны параллельны, а две другие − непараллельны. Параллельные стороны называются основаниями, а две другие стороны −боковыми сторонами.

Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией. Трапеция, у которой хотя бы один угол прямой, называется прямоугольной трапецией.

Средняя линия трапеции параллельна основаниям и равна их полусумме: \(m = \large\frac{{a + b}}{2}\normalsize,\;\;m\parallel a,\;\;m\parallel b\)

Диагонали трапеции (при условии \(a>b\)) \(p = \sqrt {\large\frac{{{a^2}b - a{b^2} - b{c^2} + a{d^2}}}{{a - b}}\normalsize} \), \(q = \sqrt {\large\frac{{{a^2}b - a{b^2} - b{d^2} + a{c^2}}}{{a - b}}\normalsize} \)

Периметр трапеции \(P = a + b + c + d\)

Площадь трапеции \(S = \large\frac{{a + b}}{2}\normalsize h = mh\) \(S = \large\frac{{a + b}}{2}\normalsize \sqrt {{c^2} - {{\left[ {\large\frac{{{{\left( {a - b} \right)}^2} + {c^2} - {d^2}}}{{2\left( {a - b} \right)}}\normalsize} \right]}^2}} \)

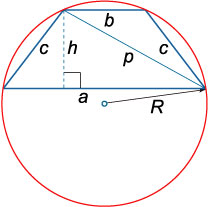
Если трапеция равнобедренная, то вокруг нее можно описать окружность.

Радиус окружности, описанной вокруг равнобедренной трапеции \(R = \large\frac{{c\sqrt {ab + {c^2}} }}{{\sqrt {\left( {2c - a + b} \right)\left( {2c + a - b} \right)} }}\normalsize\)

Диагональ равнобедренной трапеции \(p = \sqrt {ab + {c^2}} \)

Высота равнобедренной трапеции \(h = \sqrt {{c^2} - \large\frac{1}{4}\normalsize{{\left( {a - b} \right)}^2}} \)

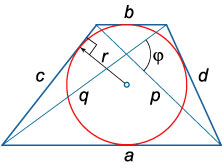
Если в произвольной трапеции сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность: \(a + b = c + d\)

Радиус вписанной окружности \(r = \large\frac{h}{2}\normalsize\), где \(h\) − высота трапеции.